supertrees using tree ranking

Constructing supertrees from trees with ranks

General background on how the supertree relates to the Open Tree of Life project

The overall goal of the project is to summarize what is known about phylogenetic relationships in a transparent manner with a clear connection to analyses and the published studies that different clads. Comprehensive coverage of published phylogenetic statements is a very long term goal which would require work from a large community of biologists. The short-term goal for the supertree presented on the tree browser is to summarize a small set of well-curated inputs in a clear manner.

We hope that this tree (and its many deficiencies) will inspire biologists to help fix the tree by alerting us to relevant phylogenetic statements that are missing in our set of inputs or contributing to the Open Tree effort in other ways. We have built tools to support 2 types of feedback:

1. Our phylogenetic study curator tool for adding new input trees.
2. Clade-linked issue reports. Click on "See comments" on a node of the tree, such as the Tetrapoda node to see a conversation that is tied to a particular phylogenetic grouping. Full issue-tracking features for that conversation (e.g. notifications, authenticated comments, tagging, closing of the issue) are supported using GitHub issues system. This issue on GitHub contains the thread about the groupings shown at the Tetrapoda node linked above.

Of course, emailing comments is another way to provide feedback (see the opentreeofliife group for general comments and this list for software issues).

Requirements of the supertree operation

Note: MTH put together this list. #3 may not be agreed upon by all participants.

1. produce a full supertree: The set of taxa associated with leaves of the supertree is the set of "terminals" in the taxonomic input.
2. the tree should display (in the sense described here) as many edges from the curated input trees as possible . If the scoring criterion was a count of the number of groupings, then this would surely by an NP-hard problem REF needed. 1. ranked trees property: For simplicity of implementation, we use a tree-based ranking system to resolve conflicts for simplicity. 2. taxonomy last property: the taxonomy is the lowest ranked input
3. Display no unsupported groupings sensu the definition describe in this doc.
4. this one definitely needs some work: we might want some statement about the placement of groups that appear in only one source tree. Perhaps: when there is a large set of attachment points to which a group can be attached and still display the same set of input tree edges, then the group should be attached at the point closest to the root that is consistent with these displayed set. This placement is in the spirit of the Adams consensus of all of the attachment points.

other assumptions:

1. the tips of all input trees have been mapped to a common taxonomy (a pruned version of OTT in our case),
2. if more than one species maps to the same OTT ID, then the tree has been pruned until this is not the case.
3. if a tip maps to a higher taxon in OTT and another tip in the tree maps to taxon within the higher taxon, then one of the tips has been pruned (process repeated until the condition no longer applies).
4. labels of internal nodes in the input phylogeny are ignored by the supertree algorithm.
5. any redundant nodes (nodes of out-degree=1) have been suppressed.
6. all trees are rooted.

The taxonomic input is a pruned version of OTT created by reading in OTT (2.8) and pruning taxa that have certain flags Needs documentation!

algorithmic implications

The strong preference for grouping based on tree-ranking simplifies the supertree construction problem considerably.

Conjecture 1: The set of equally optimal trees (A) can be expressed as a forest of rooted phylogenetic networks, but (B) may not necessarily be expressable as a tree.

We will use the phrase "phylogenetic graph" to refer to a direct graph in which each connected component in which each connected component is a phylogenetic network (contains no directed cycles).

One can think of an incompletely resolved tree (a tree with polytomies) as representing the set of trees that can be obtained by fully resolving the polytomies (but retaining all groupings in the original trees).

The proof of (B) is straightforward. Consider the inputs:

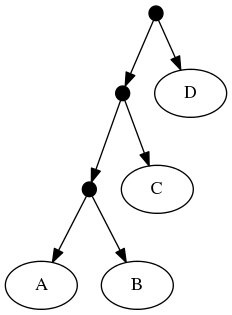
The follwing set of trees that can be produced by taking the union of all resolutions of both of these trees:

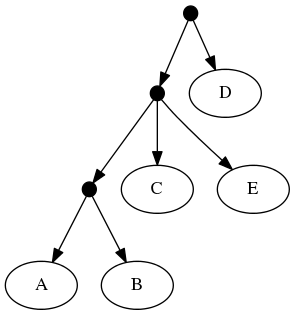
Or by the phylogenetic network:

But not by the set of all trees that resolve the:

or any other tree because no tree displaying the rooted triplet ((A,C),B) is a valid solution.

We hope to prove part (A) of the conjecture by describing an algorithm.

"phyloreference placement"

Consider the case of an clade or single tip referred to as X is present in an input tree, t, but:

1. no taxa assigned to X a have been added to a directed phylogengetic network, N, and
2. N has all of the other taxa from in t a connected component.
3. the edge that connects X to the rest of t is not a edge adjacent to a root with out-degree=2.

The procedure that we will call "phyloreference placement" of X consists of:

1. generating a phylogenetic definition of the node or edge that X attaches to in t which uses as designators all of the relevant leaf taxa t except the taxa under X. This could be the definition of an edge (if the parent of X is bifurcating, or a node if the parent of X is a polytomy). In the case of a node definition the phyloreference is a statement of all of the taxa that descend from the node. For an edge definition, the descendant taxa of the edge and the "outgroup" are all included in the definition.
2. looking for a corresponding edge, path, or node in N based on the definition: 1. if an edge is found, X is added to the N creating a parent for it that bisects the edge; 2. if a node is found, then it is treated as the parent to X 3. if a path is found, then X is attached by creating a loop from the start node of the path to the end node and and adding a parent for X along that path. 4. if the object defined by the phyloreference for X does not exist, then the descendant leaf set of the grandparent of X is calculated. The LICA of these leaves in N will serve as the parent of the X when it is attached to the graph.

Conjecture 2: prune then "phylogenetic placement" works for single-source clades.

If there exists a node X in one input trees, t such that all of the leaves correspond to taxa which are not found in any of the of the input trees other than t, then we call the group defined by X a "single-source clade".

If we were to find the phylogenetic graph that represents the optimal solution it would be identical to the solution that one could obtain by:

1. pruning the single-source clade from the input tree,
2. finding the optimal phylogenetic graph for the pruned inputs,
3. using phyloreferencing placement to attach X to the graph.

technical links

See this page for one discussion of a scoring criterion which MTH thinks could be viewed as a criterion that the automated "tree synthesis" attempts to solve. This page will discuss some algorithmic considerations about this style of synthesis.