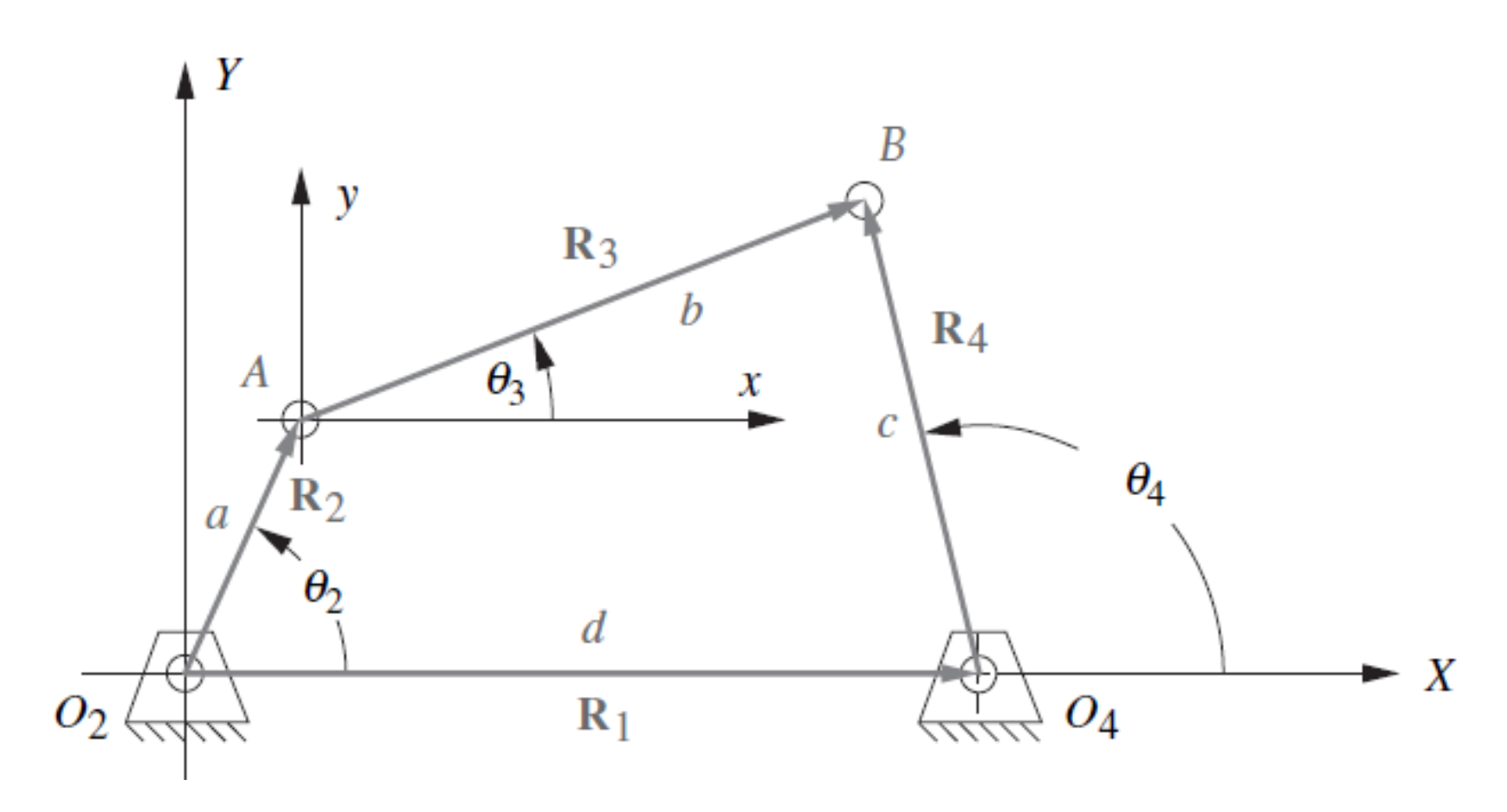
This Python Notebook is a tool to calculate the kinematic model (position, velocity and acceleration) for a 4-bar mechanism in several configurations
- User has to input the size of the 4 linkage bars
$(a, b, c, d)$ - Linkage bars are classified based on their sizes
-
$S:$ Shortest member -
$L:$ Longest member -
$P, Q:$ Remaining members
-
- Grashof condition is applied in order to classify the 4-bar mechanism
-
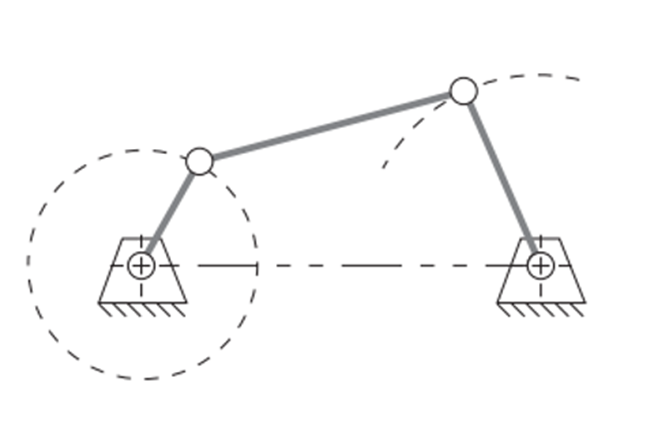
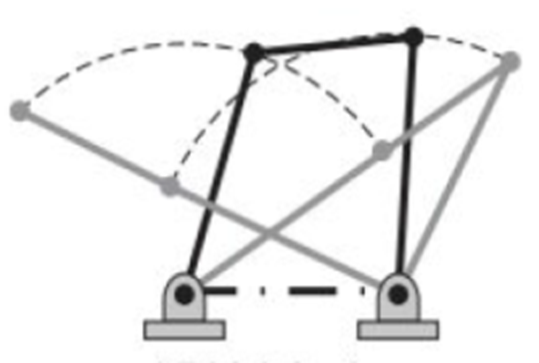
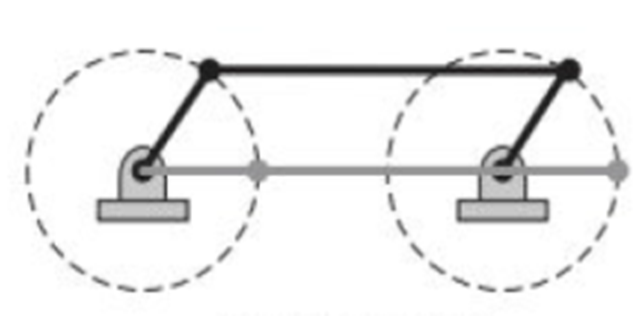
Crank and Rocker Mechanism: Occurs when the ground link
$d$ is the shortest member$(S)$
-
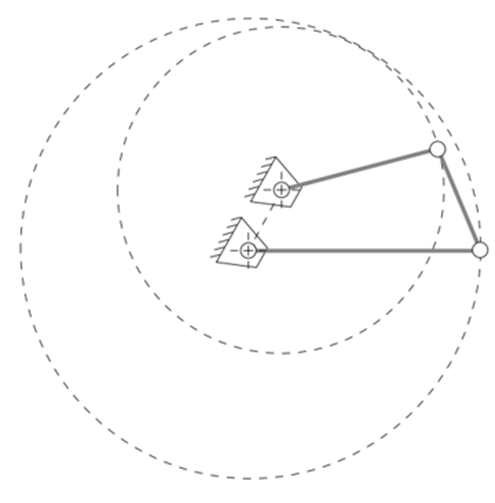
Double Crank Mechanism: Occurs when linkage bars
$a$ or$c$ are the shortest member$(S)$
-
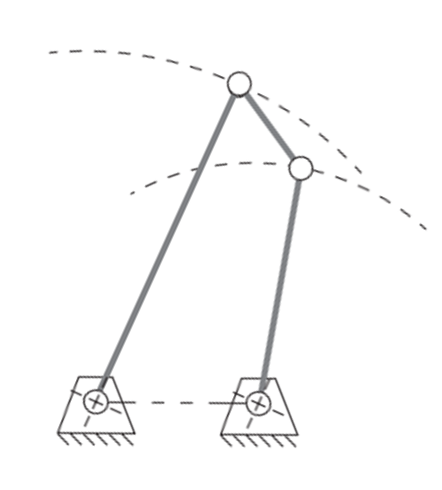
Double Rocker Mechanism: Occurs when the couples link
$b$ is the shortest member$(S)$
- User hast to enter the initial angular position, angular velocity and angular acceleration. In addtion, time and time-step have to be defined.
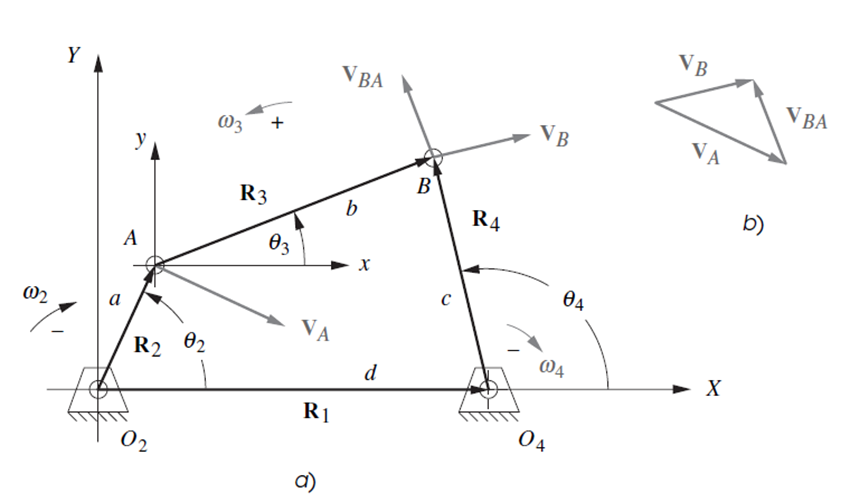
- The kinematics models is derived using the vectorial representation of the 4 bar mechanism, getting the Freudenstein's Equations
Position analysis is performed solving the following equations. One of the three angles had to have been defined by the user, so it would be a system of two equations and two unknowns.
Real Part
Imaginary Part
Due to the angles are related with trigonometric functions, Newton-Raphson method is used for solving the equations.
The velocity analysis is performed based on the following systems of linear equations
Real Part
Imaginary Part
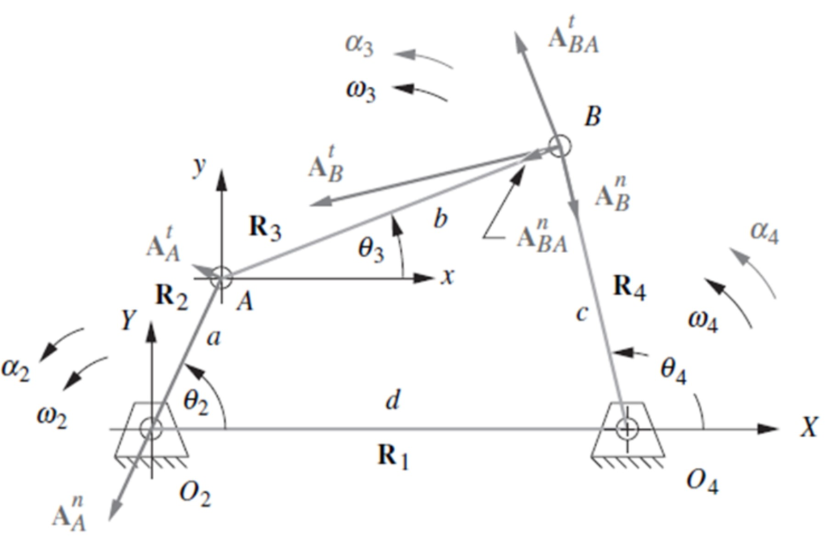
The acceleration analysis is performed based on the following systems of linear equations
Real Part
Imaginary Part