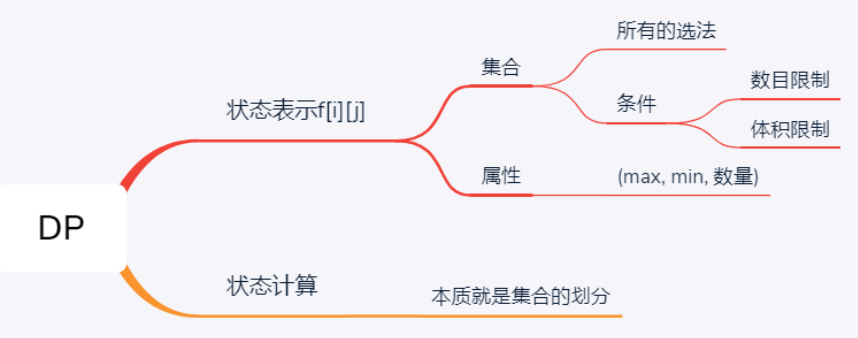
DP从两个方面考虑:
状态表示:
用几维去表示状态,这里的状态包括集合以及属性
集合:所有的选法,以及需要满足的条件
属性:min、max、count
状态计算:
状态转移方程:集合的划分,该状态怎么从之前状态推出来
优化:对代码、方程进行等价变形
n个物品,背包体积V,每个物品两个属性,v-体积,w-权重,每件物品只能装一次。
目标:选出来的物品都总价值最大
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int dp[N][N],n,m;
int v[N],w[N];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>v[i]>>w[i];
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
dp[i][j]=dp[i-1][j];
if(j>=v[i]) dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i]);
}
}
cout<<dp[n][m];
return 0;
}优化:一维储存
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int dp[N],n,m;
int v[N],w[N];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>v[i]>>w[i];
}
//同样更新n轮,每次只保存j的信息
for(int i=1;i<=n;i++){
//逆序循环j,如果正序,会污染dp[i-1][j-v[i]]的值,因为我们想要的是第i-1轮,但是当我们更新第i轮的时候,由于j-v[i]小于j,所以我们会先更新j-v[i],导致它变成了dp[i][j-v[i]],所以要倒序更新
for(int j=m;j>=v[i];j--){
dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
}
}
cout<<dp[m];
return 0;
}每件物品可无限次装入。
//朴素好理解但TLE版本
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int dp[N][N],n,m;
int w[N],v[N];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
//不再将状态划分为两份,而是划分为k+1份,其中k=0包括了上面的dp[i-1][j],上面是求两份的最大值,现在求k+1份最大值
for(int k=0;k*v[i]<=j;k++){
dp[i][j]=max(dp[i][j],dp[i-1][j-k*v[i]]+k*w[i]);
}
}
}
cout<<dp[n][m];
return 0;
}//优化1.0版本--找规律
dp[i][j]=max(dp[i-1][j],dp[i-1][j-v]+w....)
dp[i][j-v]=max(dp[i-1][j-v],dp[i-1][j-2*v]+2*w)
上面比下面多了一个w,所以dp[i][j]=max(dp[i-1][j],dp[i][j-v[i]]+w[i])
for(int i = 1 ; i <=n ;i++)
for(int j = 1; j <=m ;j++)
{
f[i][j] = f[i-1][j];
if(j-v[i]>=0)
f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
}//优化2.0版本--一维
for(int i = 1 ; i <=n ;i++)
//与01背包只有循环的顺序不一样
for(int j = v[i] ; j <=m ;j++)
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}每个物品的数量不一致,各有si件。
//暴力写法,与完全背包一样,唯一的限制是k<=s[i];
数据范围
0<N,V≤100
0<vi,wi,si≤100
for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>s[i];
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
for(int k=0;k*v[i]<=j&&k<=s[i];k++)
dp[i][j]=max(dp[i][j],dp[i-1][j-k*v[i]]+k*w[i]);
}
}
cout<<dp[n][m];/*优化1.0--二进制优化
多重背包转移01背包问题
将多重背包进行分组,假设s=1000
可以用1,2,4,8,...,2^k C 可以完全表示s(C是常数)
首先可以凑出来0-2^k的所有值,之后加上C,可以凑出任意s*/
这样做的目的是,将s拆分为logs,1个多重背包问题就变成了logs个01背包问题,总的时间复杂度是n*v*logs,比之前的n*v*logs低
N*logs个01背包问题,开数组注意
#include<bits/stdc++.h>
using namespace std;
const int N=12010;
int f[N],n,m;
struct Good{
int v;
int w;
};
int main(){
cin>>n>>m;
vector<Good> goods;
for(int i=0;i<n;i++){
int v,w,s;
cin>>v>>w>>s;
for(int k=1;k<=s;k*=2){
s-=k;
goods.push_back({k*v,k*w});
}
if(s>0) goods.push_back({s*v,s*w});
}
for(auto g:goods){
for(int j=m;j>=g.v;j--){
f[j]=max(f[j],f[j-g.v]+g.w);
}
}
cout<<f[m]<<endl;
return 0;
}物品有n组,每组里面有若干个,每组里只能选一个。
//与01背包问题类似
#include<bits/stdc++.h>
using namespace std;
const int N=110;
int dp[N];
int n,m;
int v[N][N],w[N][N],s[N];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>s[i];
for(int k=1;k<=s[i];k++){
cin>>v[i][k]>>w[i][k];
}
}
for(int i=1;i<=n;i++){
for(int j=m;j>=0;j--){
for(int k=1;k<=s[i];k++){
if(v[i][k]<=j) dp[j]=max(dp[j],dp[j-v[i][k]]+w[i][k]);
}
}
}
cout<<dp[m];
return 0;
}//给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
思路:dp[x]代表金额x所需的最小硬币数,dp[0]=0,x=1时,dp[1]=dp[0]+1
x=2时,dp[2]=dp[1]+1....dp[i]=min(dp[i], dp[i-coins[j]]+1)
金额i最小是由coins里的每个金额加上前面的合适金额构成的
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount+1,0x3f3f3f3f);
dp[0]=0;
for(int i=1;i<=amount;i++){
for(int j=0;j<coins.size();j++){
if(coins[j]<=i) dp[i] = min(dp[i], dp[i-coins[j]]+1);
}
}
return dp[amount]==0x3f3f3f3f? -1 :dp[amount];
}