README.md

1361. Validate Binary Tree Nodes

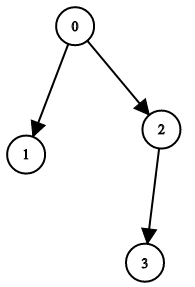
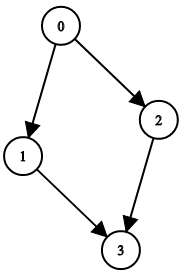
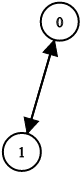
You have n binary tree nodes numbered from 0 to n - 1 where node i has two children leftChild[i] and rightChild[i], return true if and only if all the given nodes form exactly one valid binary tree.

If node i has no left child then leftChild[i] will equal -1, similarly for the right child.

Note that the nodes have no values and that we only use the node numbers in this problem.

Example 1:

Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true

Example 2:

Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false

Example 3:

Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false

Constraints:

• n == leftChild.length == rightChild.length
• 1 <= n <= 104
• -1 <= leftChild[i], rightChild[i] <= n - 1

Solutions (Rust)

1. Solution

use std::collections::HashSet;

impl Solution {
    pub fn validate_binary_tree_nodes(n: i32, left_child: Vec<i32>, right_child: Vec<i32>) -> bool {
        let mut candidates = (0..n).collect::<HashSet<_>>();
        let mut stack = vec![];
        let mut visited = HashSet::new();

        for i in 0..left_child.len() {
            if left_child[i] >= 0 && !candidates.remove(&left_child[i]) {
                return false;
            }
            if right_child[i] >= 0 && !candidates.remove(&right_child[i]) {
                return false;
            }
        }

        if candidates.len() != 1 {
            return false;
        }

        stack.push(candidates.into_iter().next().unwrap() as usize);
        visited.insert(stack[0]);

        while let Some(i) = stack.pop() {
            if left_child[i] >= 0 {
                if visited.insert(left_child[i] as usize) {
                    stack.push(left_child[i] as usize);
                } else {
                    return false;
                }
            }
            if right_child[i] >= 0 {
                if visited.insert(right_child[i] as usize) {
                    stack.push(right_child[i] as usize);
                } else {
                    return false;
                }
            }
        }

        visited.len() == n as usize
    }
}