https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
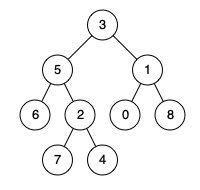
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。
- 递归
- 阿里
- 腾讯
- 百度
- 字节
这道题目是求解二叉树中,两个给定节点的最近的公共祖先。是一道非常经典的二叉树题目。
我们之前说过树是一种递归的数据结构,因此使用递归方法解决二叉树问题从写法上来看是最简单的,这道题目也不例外。
用递归的思路去思考树是一种非常重要的能力。
如果大家这样去思考的话,问题就会得到简化,我们的目标就是分别在左右子树进行查找 p 和 q。 如果 p 没有在左子树,那么它一定在右子树(题目限定 p 一定在树中), 反之亦然。
对于具体的代码而言就是,我们假设这个树就一个结构,然后尝试去解决,然后在适当地方去递归自身即可。 如下图所示:
我们来看下核心代码:
// 如果我们找到了p,直接进行返回,那如果下面就是q呢? 其实这没有影响,但是还是要多考虑一下
if (!root || root === p || root === q) return root;
const left = lowestCommonAncestor(root.left, p, q); // 去左边找,我们期望返回找到的节点
const right = lowestCommonAncestor(root.right, p, q); // 去右边找,我们期望返回找到的节点
if (!left) return right; // 左子树找不到,返回右子树
if (!right) return left; // 右子树找不到,返回左子树
return root; // 左右子树分别有一个,则返回root如果没有明白的话,请多花时间消化一下
- 用递归的思路去思考树
代码支持: JavaScript, Python3
- JavaScript Code:
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {TreeNode} p
* @param {TreeNode} q
* @return {TreeNode}
*/
var lowestCommonAncestor = function (root, p, q) {
if (!root || root === p || root === q) return root;
const left = lowestCommonAncestor(root.left, p, q);
const right = lowestCommonAncestor(root.right, p, q);
if (!left) return right; // 左子树找不到,返回右子树
if (!right) return left; // 右子树找不到,返回左子树
return root; // 左右子树分别有一个,则返回root
};- Python Code:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if not root or root == p or root == q:
return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if not left:
return right
if not right:
return left
else:
return root复杂度分析
令 h 为树的高度。
- 时间复杂度:$O(N)$
- 空间复杂度:$O(h)$
如果递归的结束条件改为if (!root || root.left === p || root.right === q) return root; 代表的是什么意思,对结果有什么样的影响?
大家对此有何看法,欢迎给我留言,我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库:https://github.com/azl397985856/leetcode 。 目前已经 37K star 啦。
大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。