-
Notifications
You must be signed in to change notification settings - Fork 15
Types and Programming Languages Chapter 10 An ML Implementation of Simple Types

Recap - where even are we? We've looked at typing rules for arith + bools, which was very boring, having only two types. We haven't implemented that yet, so this is our first type checker impl meeting, looking at lambda calc + bools.


[debate about the number of permissible assertions per test]

Leo: This is NOT London TDD Club
[all: it kinda is tho]

At this point I gave up taking notes and decided to let the code speak for itself.
Here is the implementation we ended up with.

- An implementation in Rust of the
arithsyntax and evaluation rules - An implementation in Rust of the
tyarithsyntax, evaluation and typing rules - An implementation in Rust of the
simpleboolsyntax and evaluation rules

Writing a parser was fun! I went back and did it for arith and it was really helpful, much nicer than doing tedious macros to construct terms.
Hard part was string manipulation where in ruby you've got a bunch of lovely stuff like StringScanner, in rust it's not so easy.
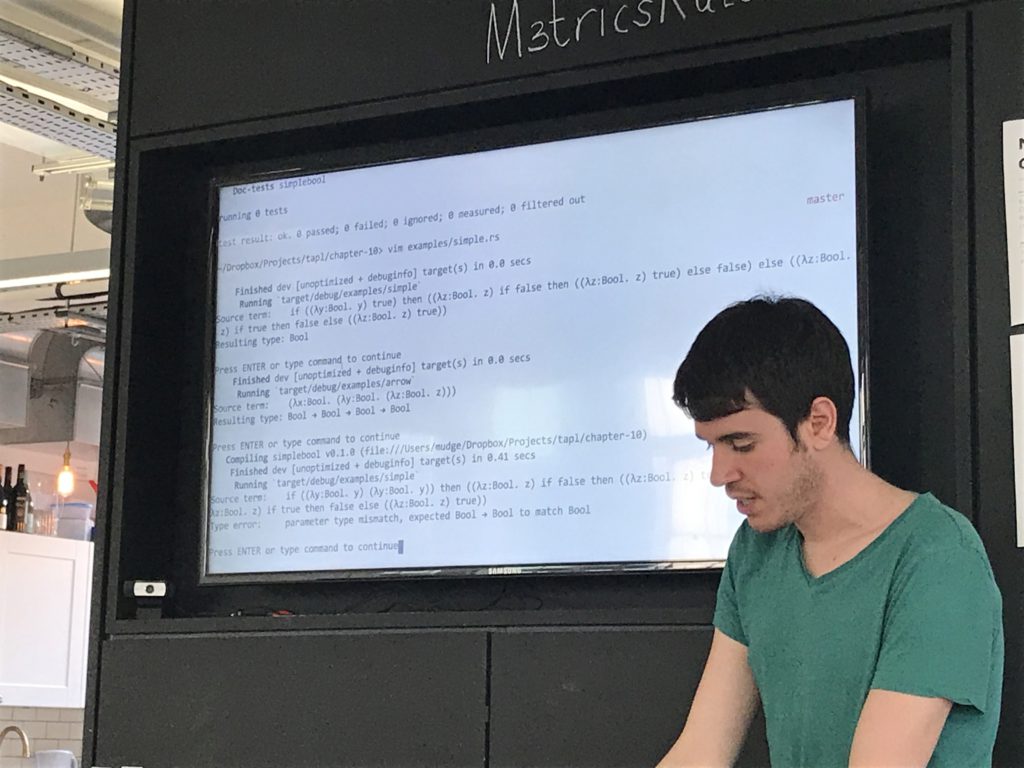
Wrote a type checker for arith - it has errors and everything that'll tell you what your problem is, assuming your problem is that your statement is badly typed.
Didn't have time for the lambda calc parser, so constructed lambda terms with macros. I really wanted to do a parser cos then you could point to exactly where the type errors are.
[Leo heckles re muts and boxes]
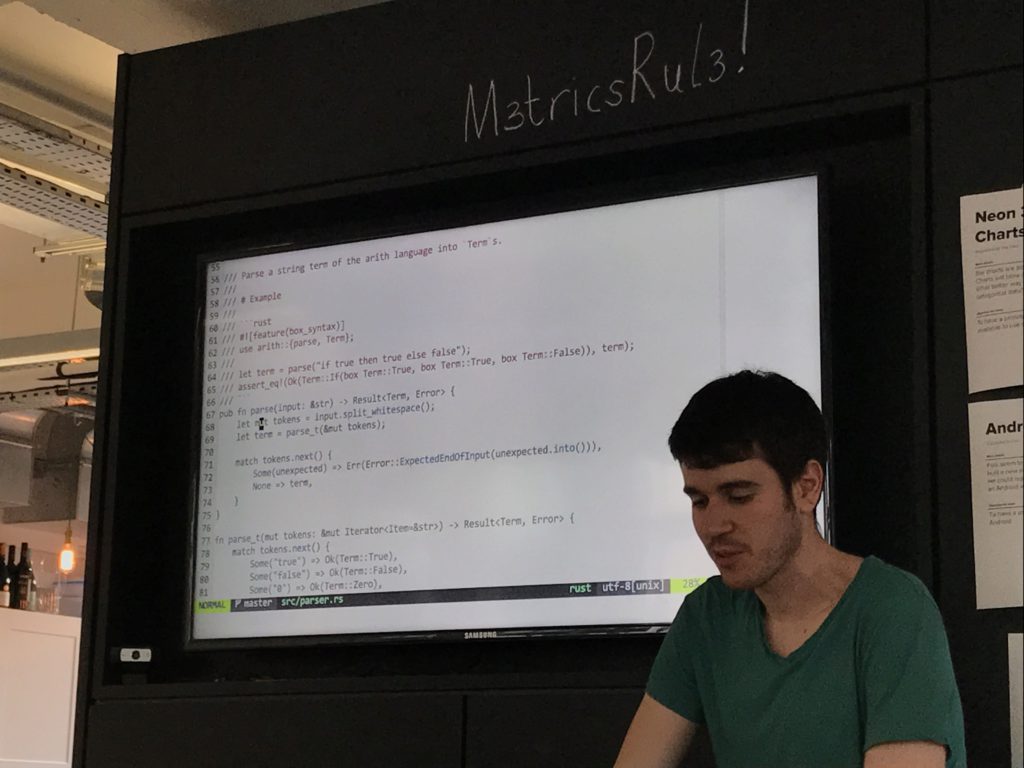
[Mudge shows us the ELDRITCH HORRORS underlying the macros]
I've focused only on the pure lambda calc and building out the bits and pieces - lexers, parsers etc.
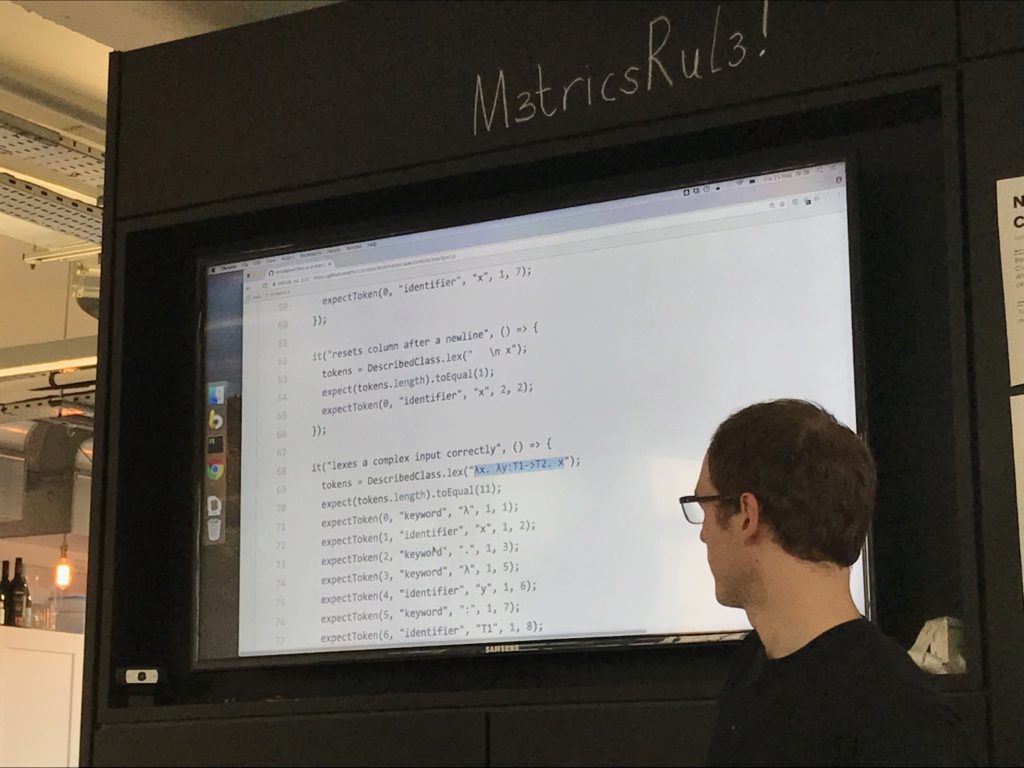
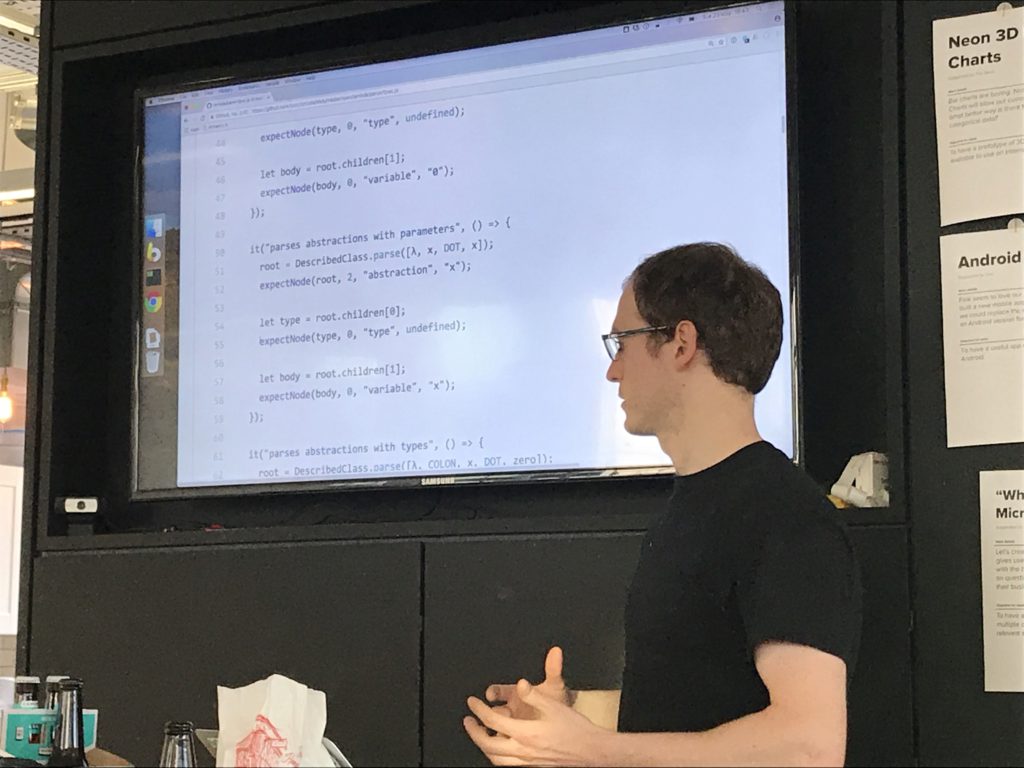
Tom: so where we had different data type for different nodes, you've got an abstract node type for all AST nodes?
Tuzz: yes. Dunno if I'd do it that way again.
I've got a debruijn-ifying process that transforms a tree, giving you a new tree with all the debruijn indices set. Also I've got a name-assigning process that generates unique names given a debruijn-indexed tree.
Spent a bit of time on a printer that doesn't produce unnecessary parentheses, so it's aware of the precedence and conventions of the grammar.
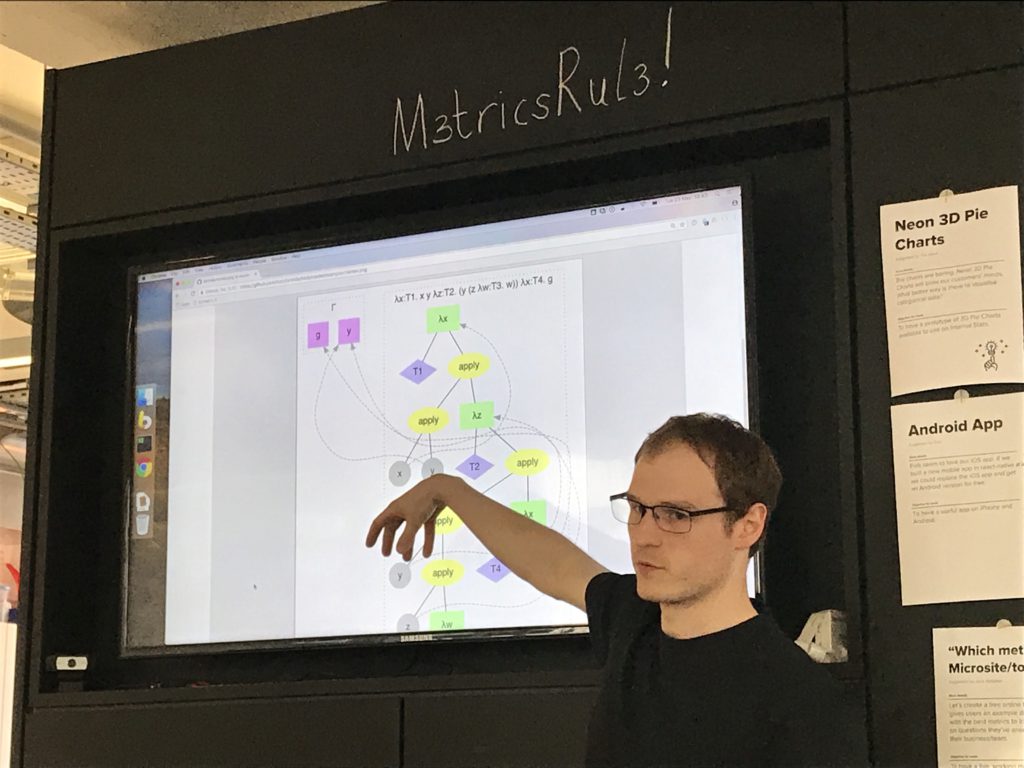
Oh yeah, and a type checker! Which I wrote last night.
A Kotlin implementation of the simply typed lambda calculus typechecker

Didn't do a parser (this book is about types after all :)), constructed AST manually (with help of functions and operator overloading; no macro-things!!).
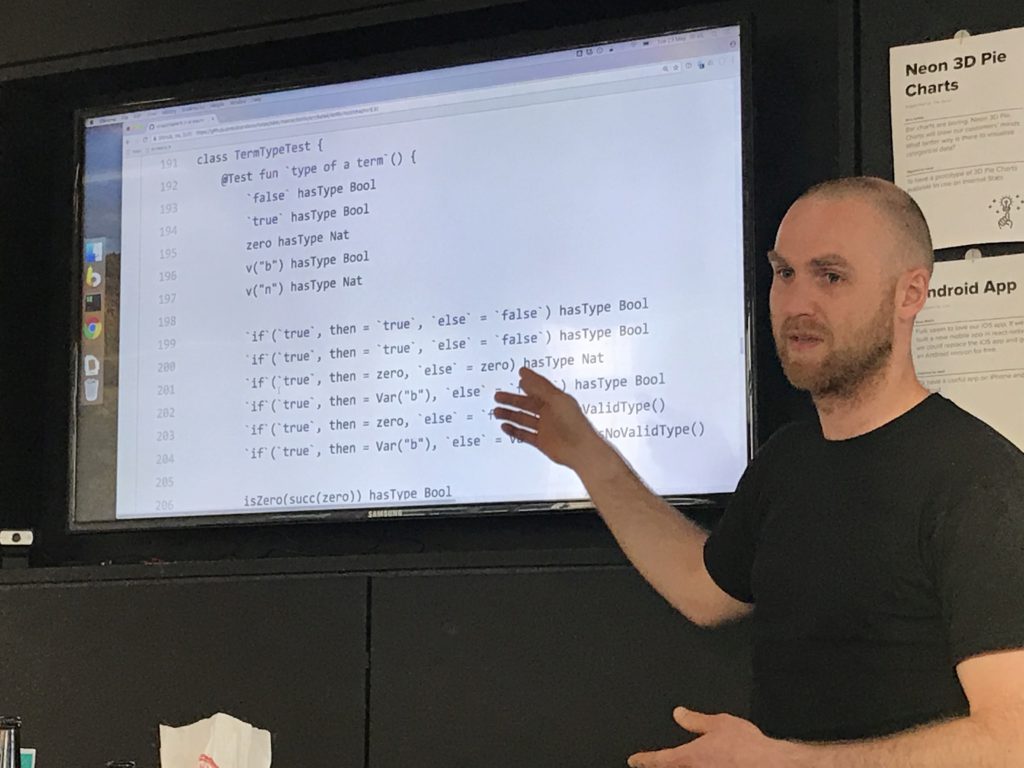
Used extension functions to make the tests more readable (in particular an aka helper to have a human-readable representation of the term being tested).
- A Python interpreter for inference rules
- Using that interpreter to implement the
simpleboolsyntax and typing rules - Jupyter notebooks which use that implementation: chapter 9 and chapter 10.
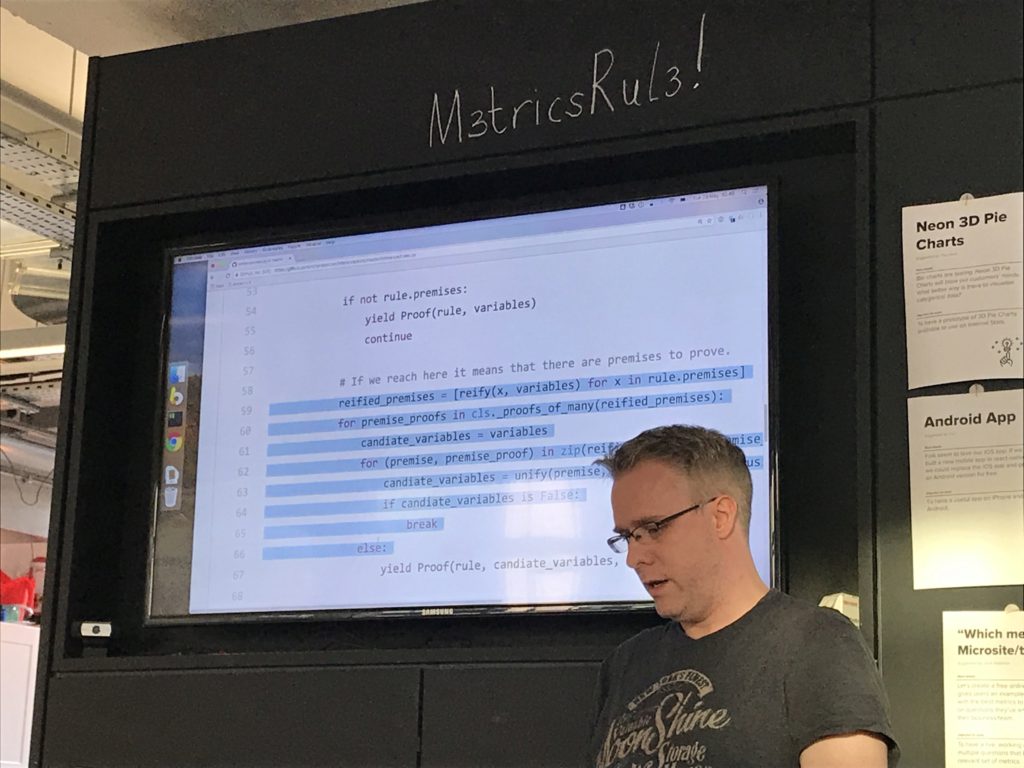
So I've not written the checker directly, I've been writing a python engine for inference rules, so basically a badly-written 10% of prolog.
It iterates over all of the rules it can find, attempting to unify the term being checked with all of the premises.
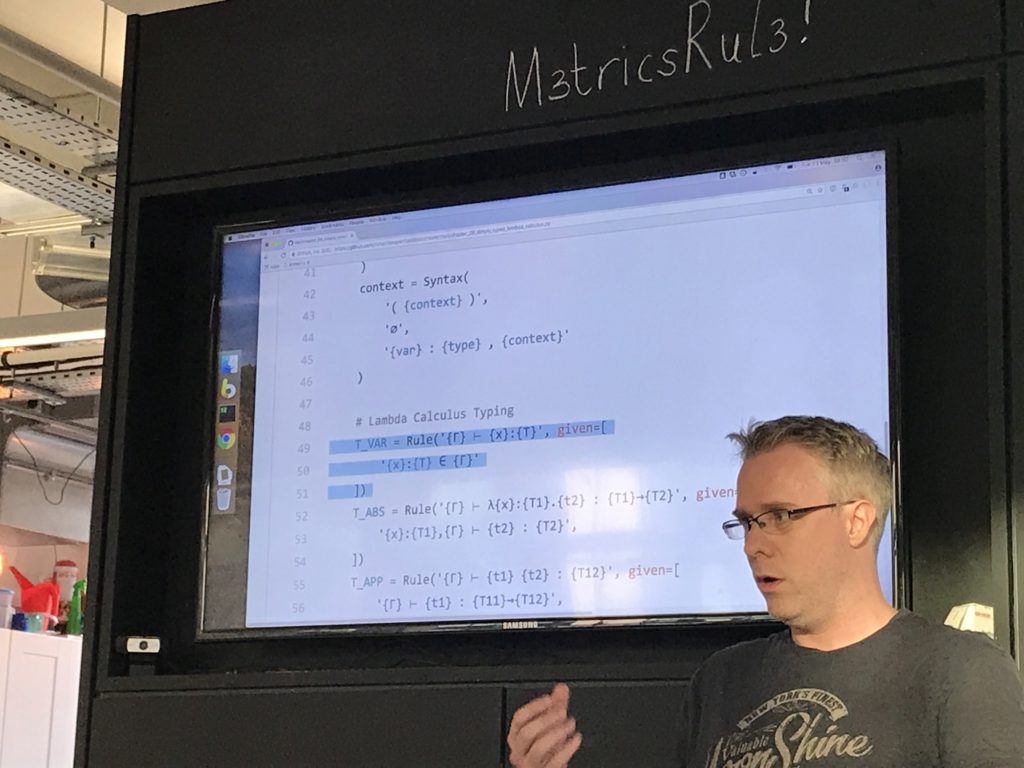
To use the inference engine you define a rules class, with two things: syntax terms and rules.

Syntax terms drive a recursive descent parser. Then you define rules with their (optionally recursive) premises.
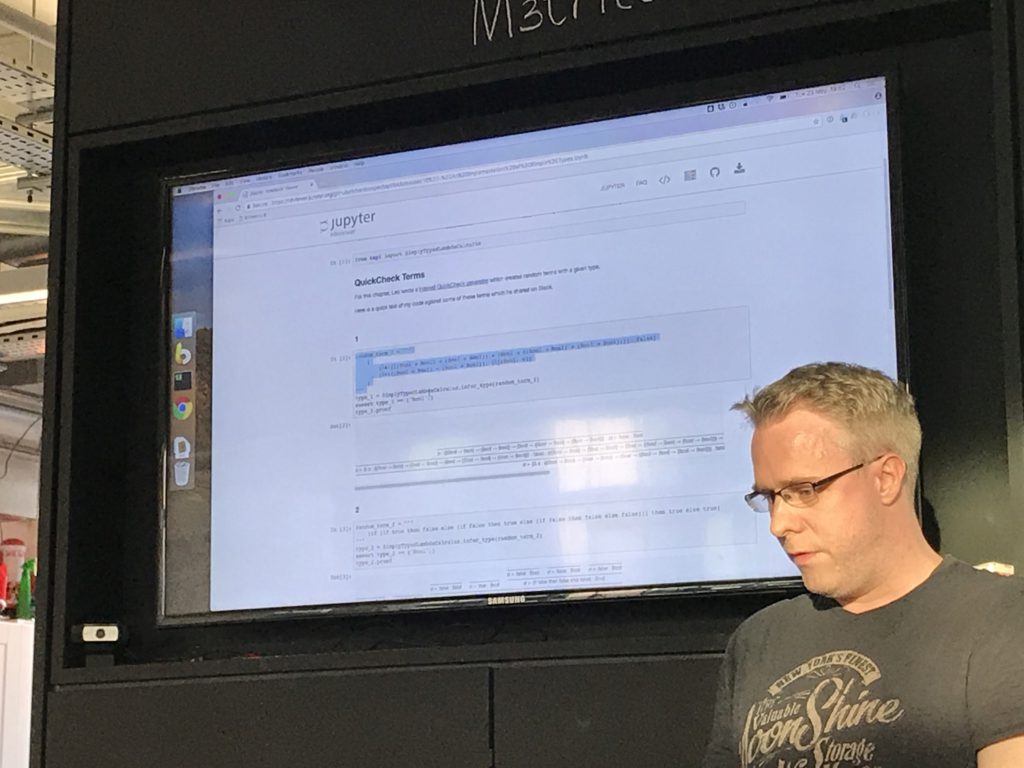
Then I've been using this output in jupyter notebooks to render the derivation trees.
[gasps of awe at enormous yet beautiful html table derivation trees]
Jupyter notebooks are really cool for annotating code with thoughts and context as you go.
- A simply typed lambda calculus typechecker in Haskell
- A QuickCheck generator for well-typed lambda calculus terms
- A verification of progress + preservation
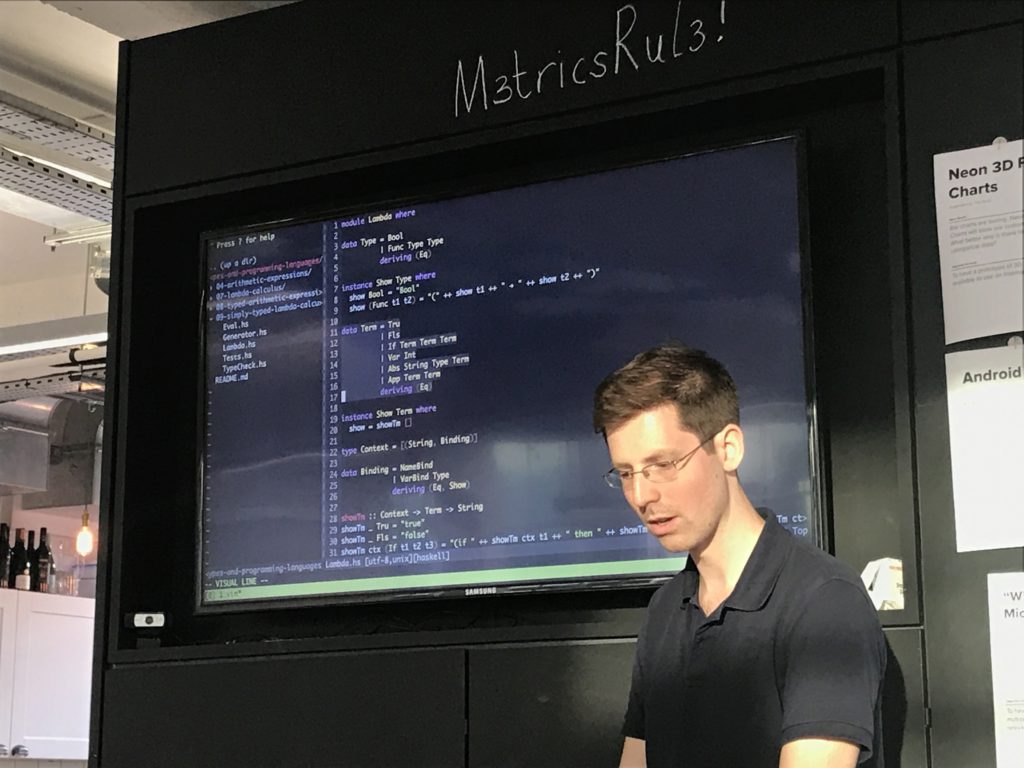
So I ported my stuff over from the untyped lambda calc. I sprinkled the syntax liberally with do notation and agonised over it greatly - I think I have the tersest type checker possible in haskell.
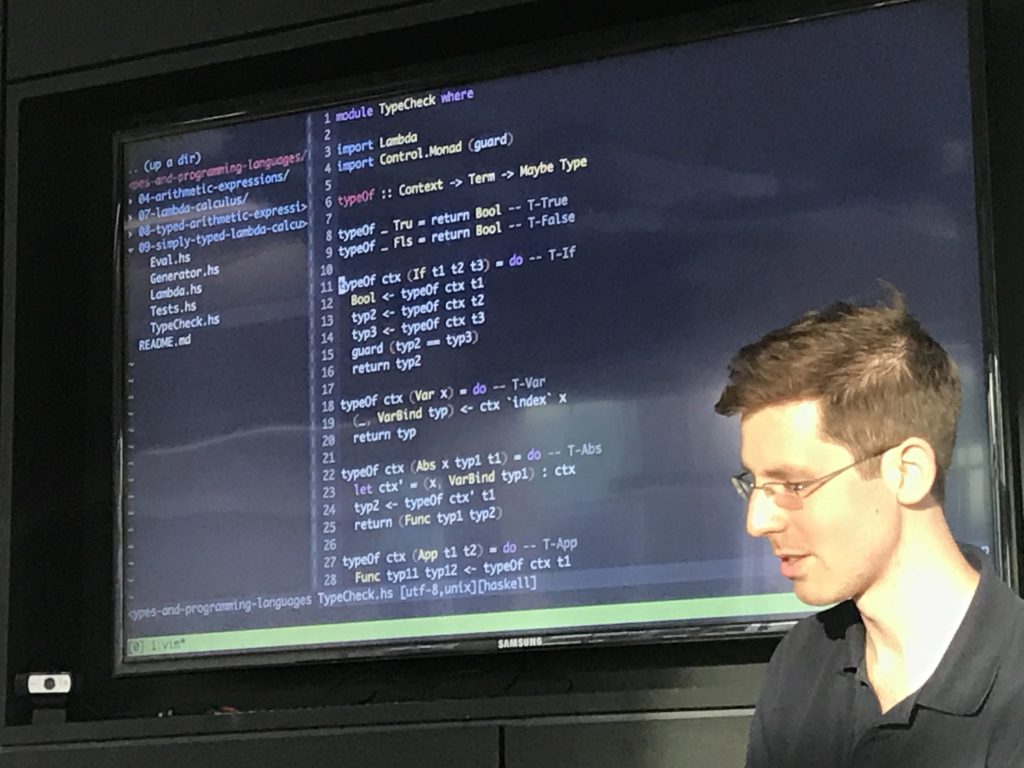
I wanted to prove properties of the checker, so headed for quickcheck. But to do this I need to be able to generate random terms. Will come back!
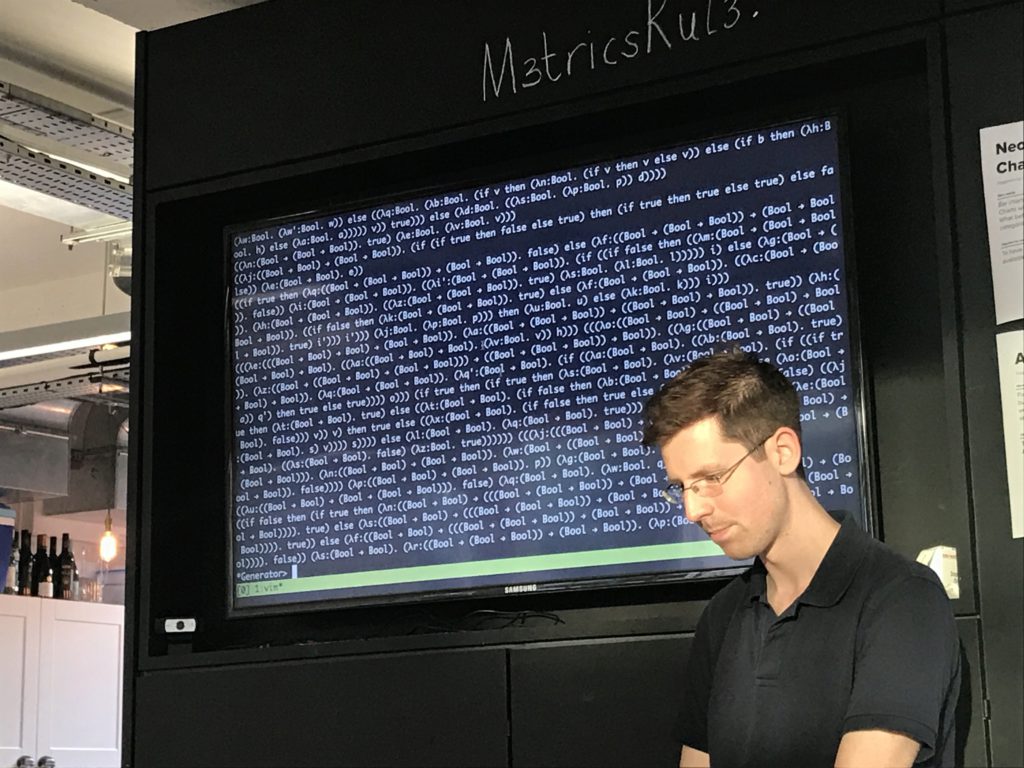
Tests I wrote were to check safety, which == progress + preservation, simply expressed in quickcheck.
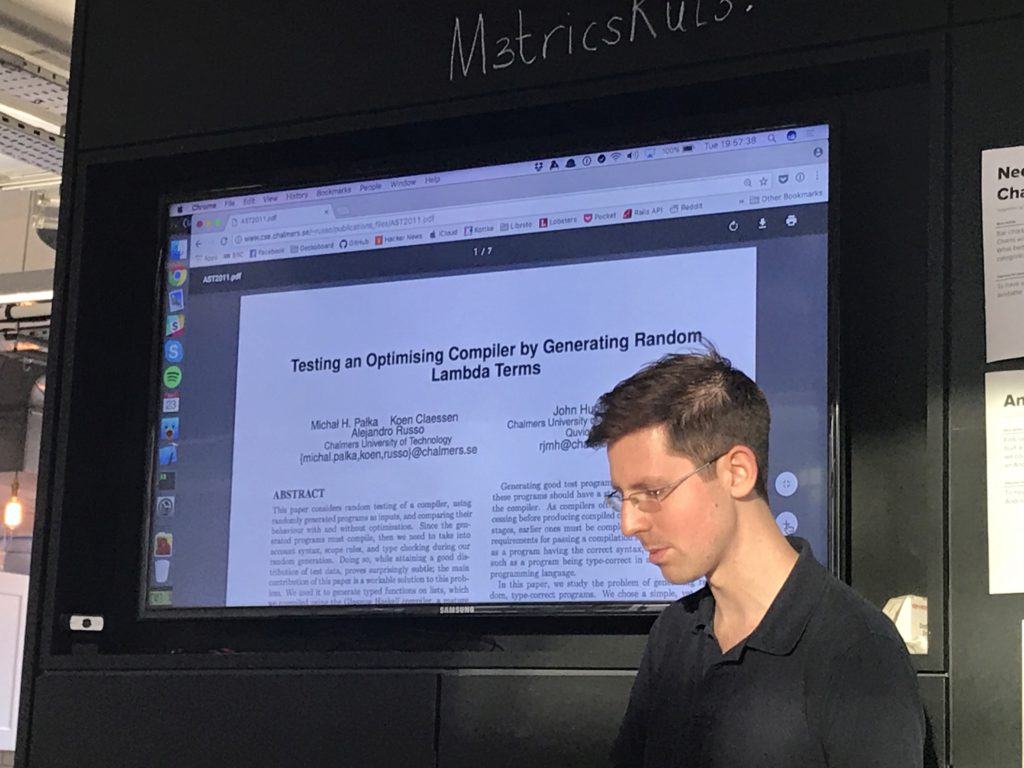
So, I need to generate well-typed lambda calc terms, and found a handy paper [LINK] that described how to do so.
First I generate a random type.
Then I feed that to a term generator, with an empty typing context, and it returns a random term of that type!
[oohs from audience]
The way this works is tricky - e.g. if I need a bool, I've got options:
true / false / if x then bool else bool / app returning bool
Use weightings for the different options to generate an interesting spread of terms.
The interesting thing from the paper was: if my goal is a random application that contains a boolean, it's easy to achieve this if you throw away the argument to the LH abstraction. So to avoid this I did [TRICK THAT I DIDN'T FOLLOW WELL ENOUGH TO RESTATE HERE].
The literature works!
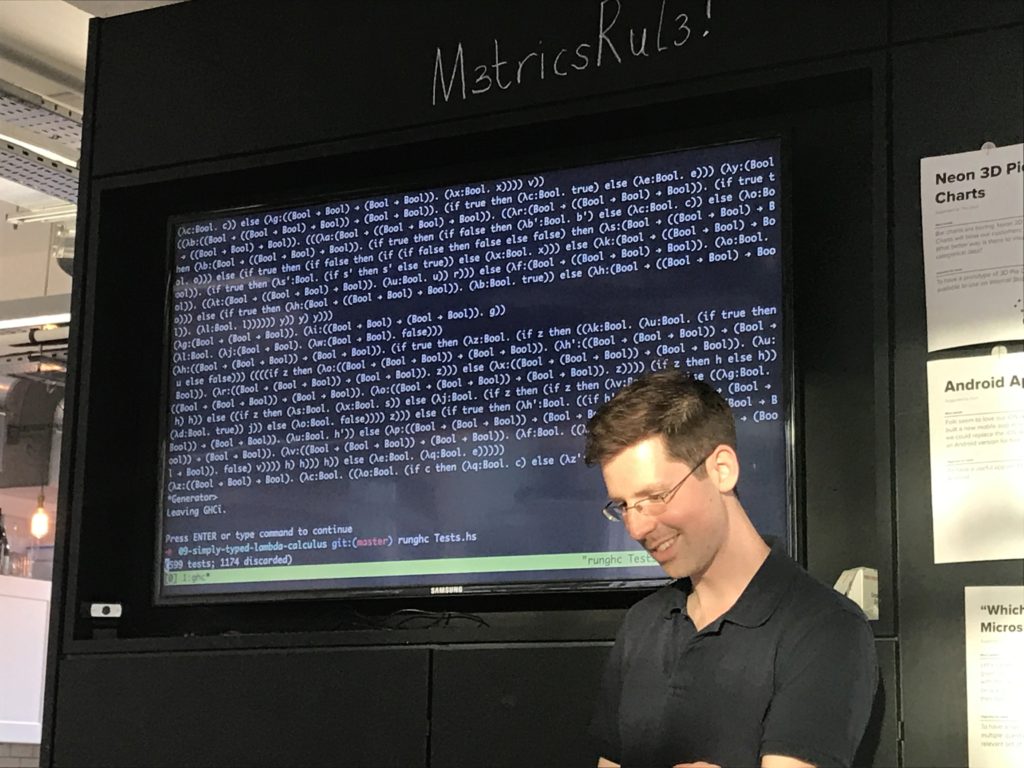
[DEMO OF QUICKCHECK INCONTROVERTIBLY PROVING THINGS]
https://github.com/zetter/tapl/tree/master/10_typed_lambda_calculus
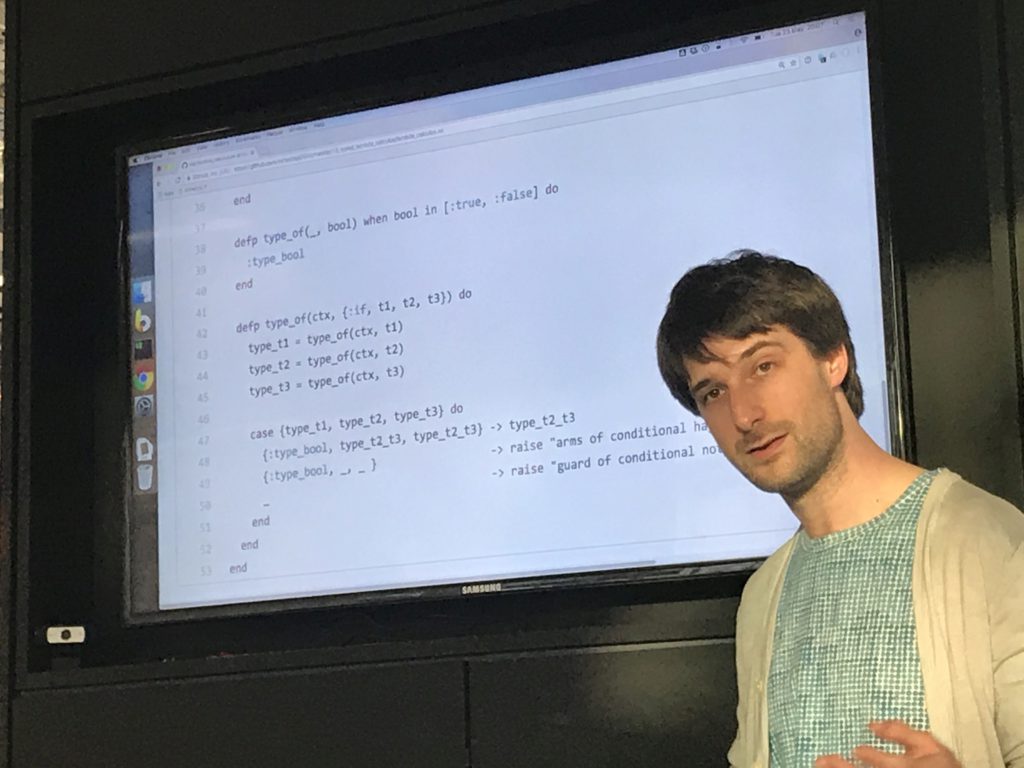
I reused the AST structure I'd previously used to represent the language, but not any code - I took debruijn indices as read since they'd been done.
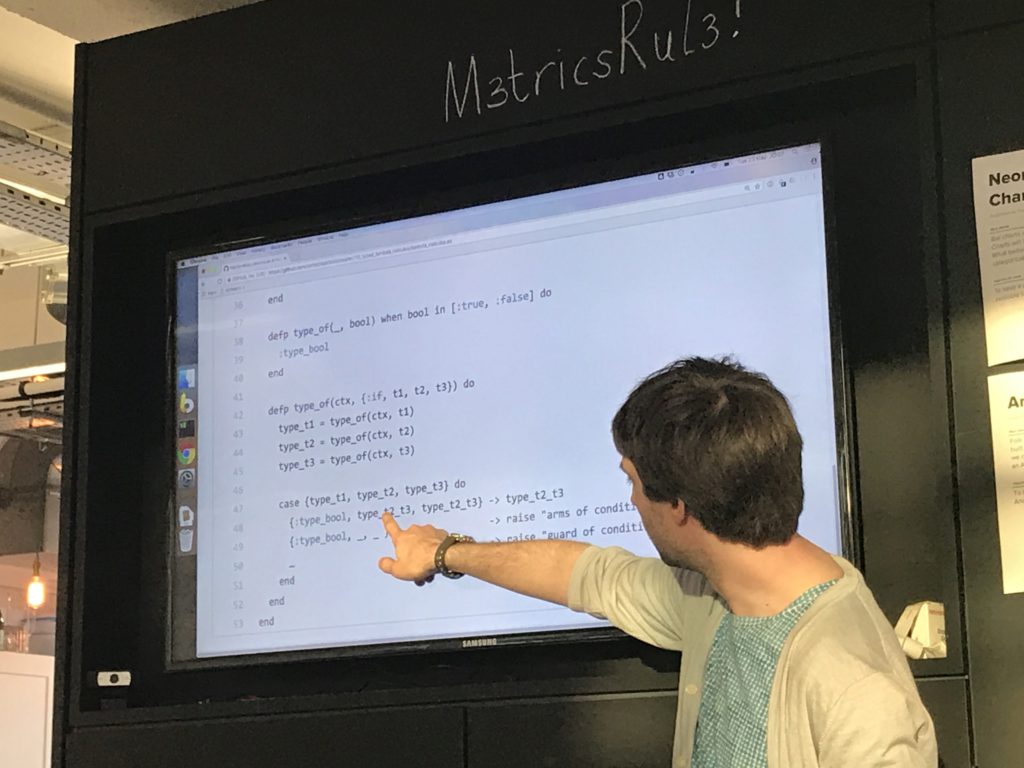
Elixir works well because of being able to both pattern on the type of term to decide what function to call, and to then pattern match on the attributes of the term in the function body to decide what to do.
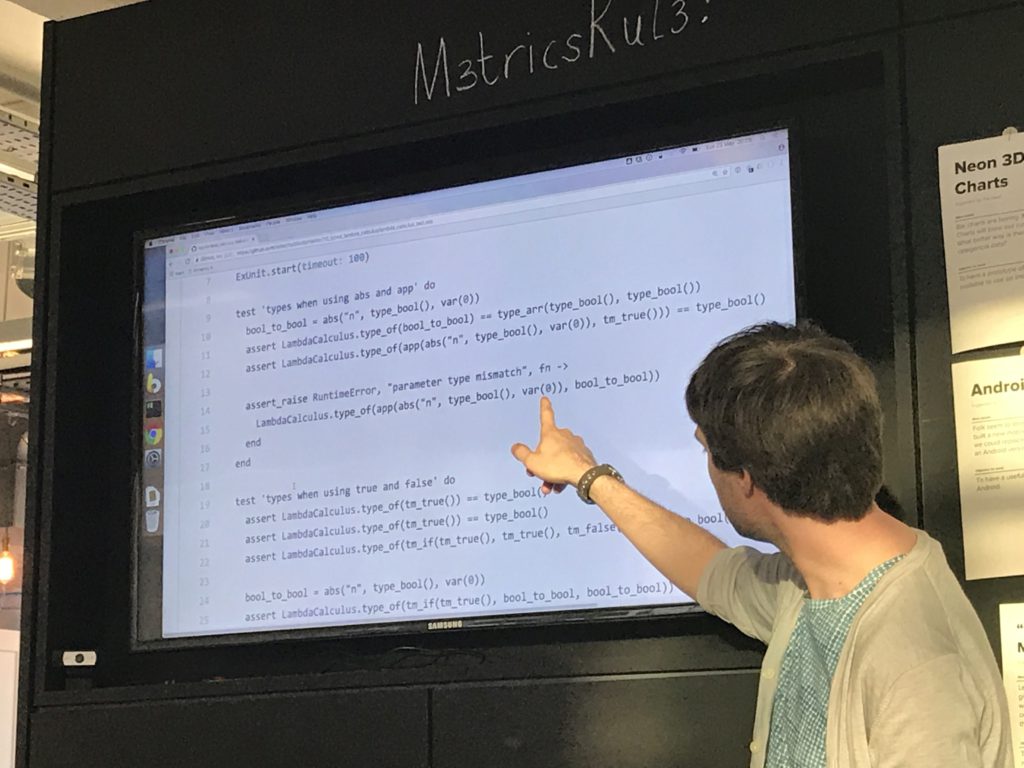
I got to use the "pin" operator (^) in elixir for the first time in one of the function bodies - usually you're assigning values when pattern matching, but this lets you pick up a previously-assigned value.
A Prolog implementation of a simply typed lambda calculus typechecker
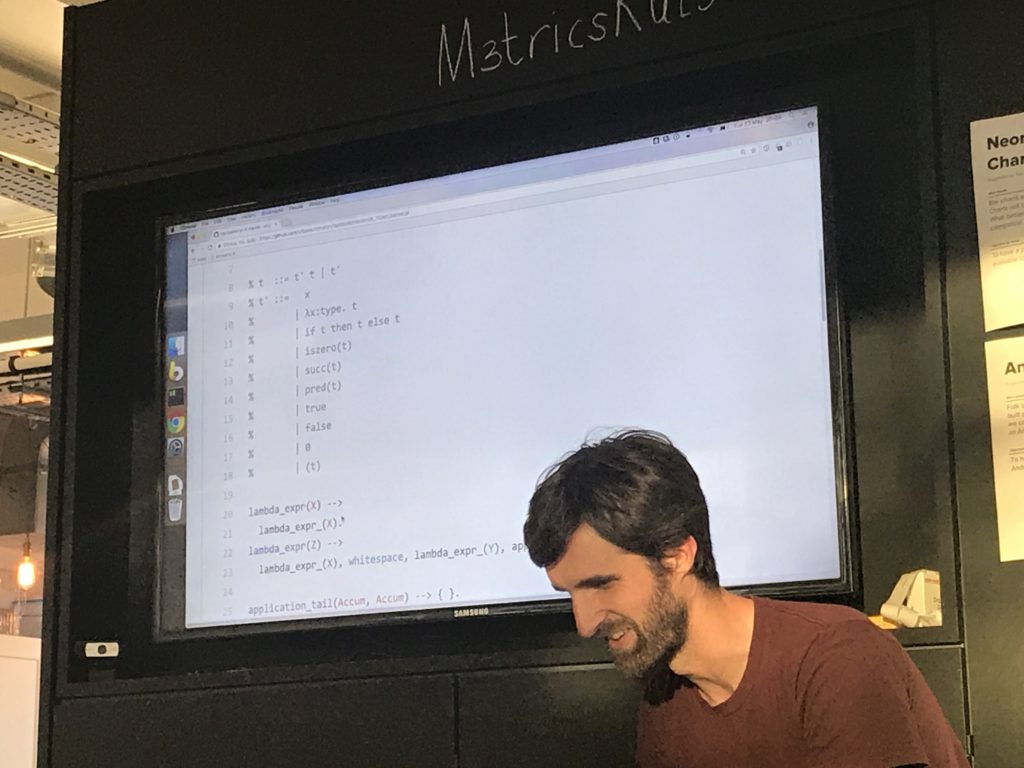
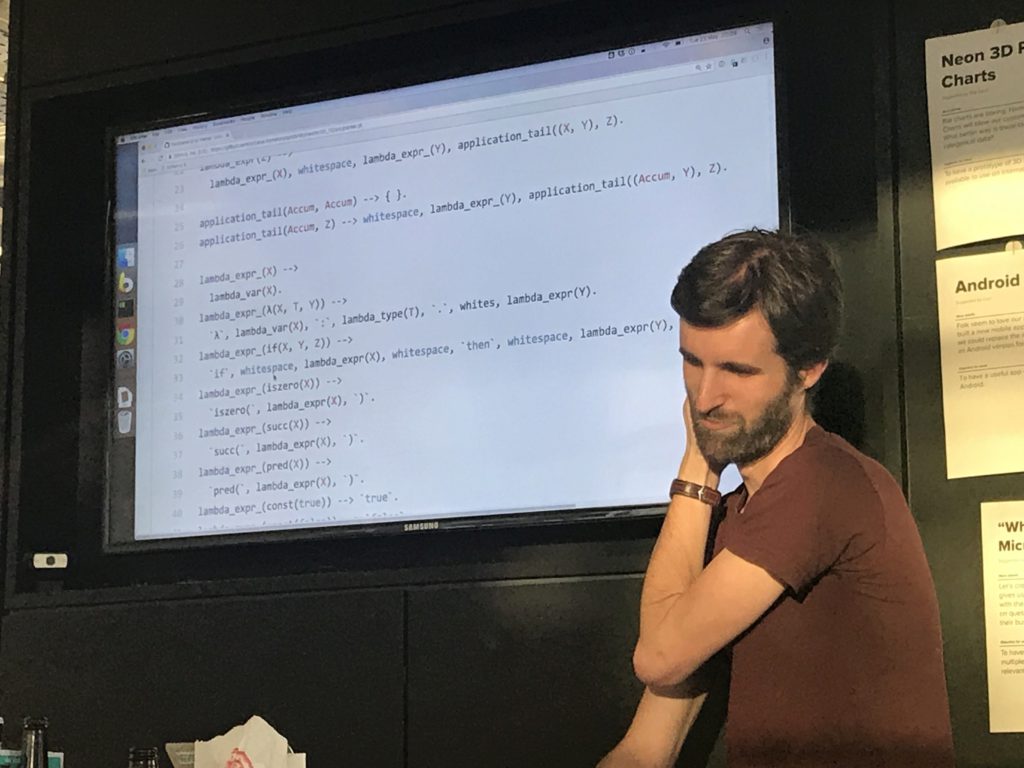
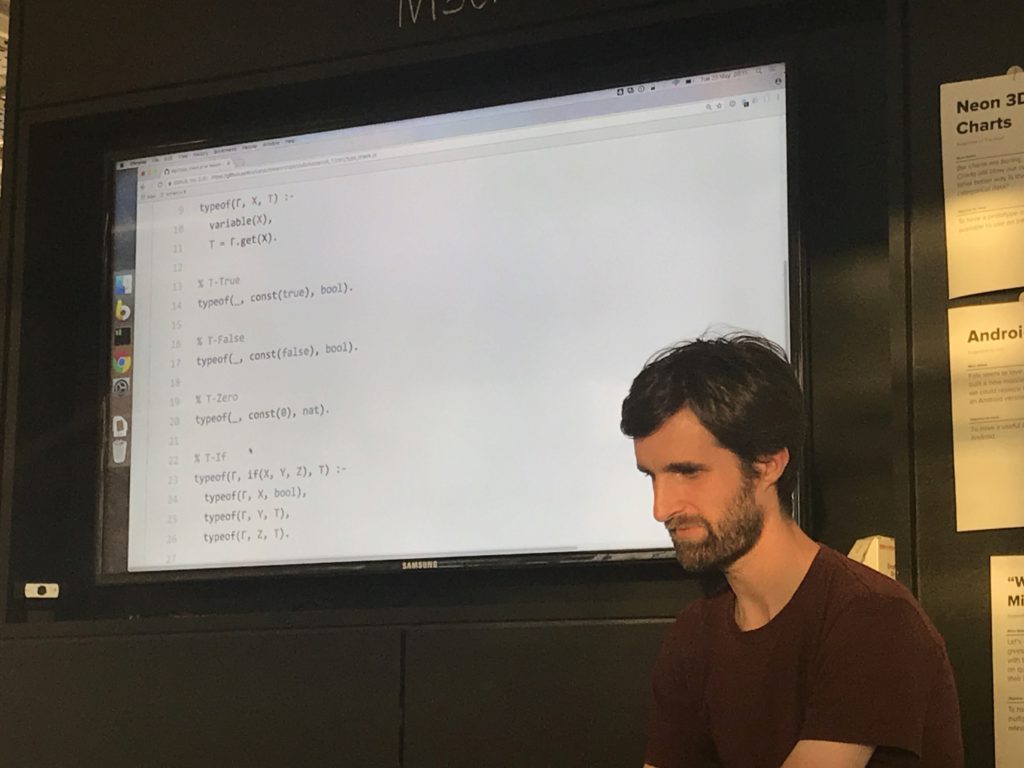
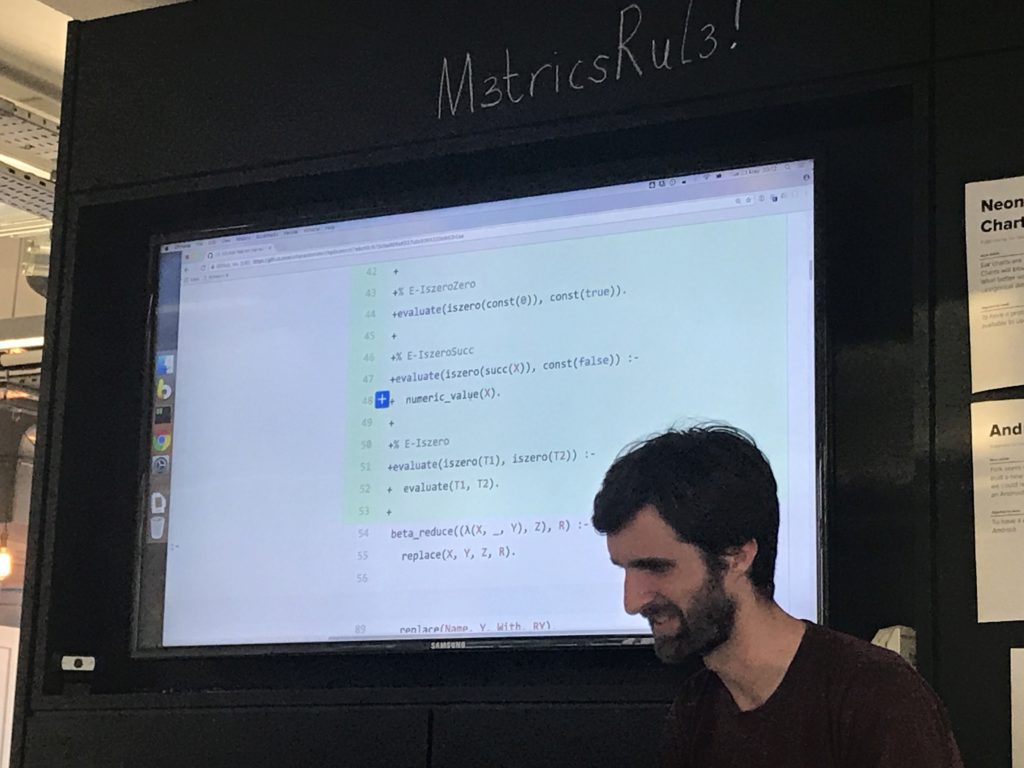
[unintelligible mumbling]
A Ruby implementation of inference rules, with typing rules for the simply typed lambda calculus
So I've done similar to Rich & Tom, implementing inference rules not in Prolog.
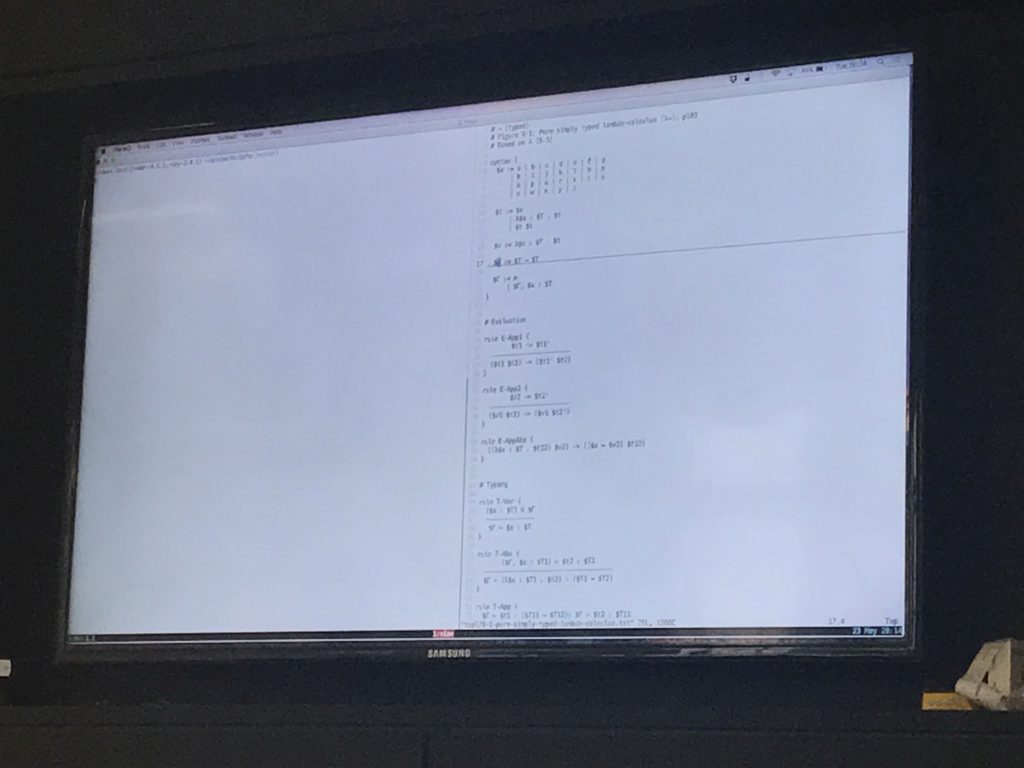
You define syntax rules and then a set of inference rules.
I was most concerned with the belongs-to relation that was sort of extrinsically defined, so I ended up defining a new set of inference rules to define what that actually meant, rather than magicking it in from nowhere.

I spent a bunch of time writing a derivation printer [pages of imposing formatting code on screen]
I also let rule systems be extended, so I can build bools on top of the pure lambda, nats on top of that, etc and so forth.
I wasn't able to prevent this issue with variable shadowing - if you append the same name to the typing context more than once, you can prove things that aren't true, and I don't know how to prevent that.
Tom: the book's solution is to say you alpha-convert terms to avoid this rather than dealing with it any other way.
How was the mobbing?
Leo: really rapid, too fast perhaps? We kinda barrelled through it.
Tom: Is the implementation pulling its weight? Is it worth it, or just treading water?
Everyone: yeah, basically. It forces us to try to comprehend stuff, and has spawned a bunch of interesting side conversations and topics.
Leo: like, I read academic literature and everything, and it did what I wanted.
Tuzz: what about the Bletchley meeting eh.
All: WHAT OF IT
[VOTE OF THANKS TO RICH FOR ORGANISING]
Next organiser then, eh?
Tuzz: Oh go on then
All: THANKS BE TO BRITISH COMPUTER SCIENTIST CHRISTOPHER PATUZZO
Is it interstitial now? Who even knows. TBD.
Tuzz: This one was quite technical but also restful - we should plough on and have a break when we feel we need one
[General assent]
- Home
- Documentation
- Choosing a Topic
- Shows & Tells
- Miscellaneous
- Opt Art
- Reinforcement Learning: An Introduction
- 10 Technical Papers Every Programmer Should Read (At Least Twice)
- 7 More Languages in 7 Weeks
- Lua, Day 1: The Call to Adventure
- Lua, Day 2: Tables All the Way Down
- Lua, Day 3
- Factor, Day 1: Stack On, Stack Off
- Factor, Day 2: Painting the Fence
- Factor, Day 3: Balancing on a Boat
- Elm, Day 1: Handling the Basics
- Elm, Day 2: The Elm Architecture
- Elm, Day 3: The Elm Architecture
- Elixir, Day 1: Laying a Great Foundation
- Elixir, Day 2: Controlling Mutations
- Elixir, Day 3: Spawning and Respawning
- Julia, Day 1: Resistance Is Futile
- Julia, Day 2: Getting Assimilated
- Julia, Day 3: Become One With Julia
- Minikanren, Days 1-3
- Minikanren, Einstein's Puzzle
- Idris Days 1-2
- Types and Programming Languages
- Chapter 1: Introduction
- Chapter 2: Mathematical Preliminaries
- Chapter 3: Untyped Arithmetic Expressions
- Chapter 4: An ML Implementation of Arithmetic Expressions
- Chapter 5: The Untyped Lambda-Calculus
- Chapters 6 & 7: De Bruijn Indices and an ML Implementation of the Lambda-Calculus
- Chapter 8: Typed Arithmetic Expressions
- Chapter 9: The Simply-Typed Lambda Calculus
- Chapter 10: An ML Implementation of Simple Types
- Chapter 11: Simple Extensions
- Chapter 11 Redux: Simple Extensions
- Chapter 13: References
- Chapter 14: Exceptions
- Chapter 15: Subtyping – Part 1
- Chapter 15: Subtyping – Part 2
- Chapter 16: The Metatheory of Subtyping
- Chapter 16: Implementation
- Chapter 18: Case Study: Imperative Objects
- Chapter 19: Case Study: Featherweight Java
- The New Turing Omnibus
- Errata
- Chapter 11: Search Trees
- Chapter 8: Random Numbers
- Chapter 35: Sequential Sorting
- Chapter 58: Predicate Calculus
- Chapter 27: Perceptrons
- Chapter 9: Mathematical Research
- Chapter 16: Genetic Algorithms
- Chapter 37: Public Key Cryptography
- Chapter 6: Game Trees
- Chapter 5: Gödel's Theorem
- Chapter 34: Satisfiability (also featuring: Sentient)
- Chapter 44: Cellular Automata
- Chapter 47: Storing Images
- Chapter 12: Error-Correcting Codes
- Chapter 32: The Fast Fourier Transform
- Chapter 36: Neural Networks That Learn
- Chapter 41: NP-Completeness
- Chapter 55: Iteration and Recursion
- Chapter 19: Computer Vision
- Chapter 61: Searching Strings
- Chapter 66: Church's Thesis
- Chapter 52: Text Compression
- Chapter 22: Minimum spanning tree
- Chapter 64: Logic Programming
- Chapter 60: Computer Viruses
- Show & Tell
- Elements of Computing Systems
- Archived pages